Trees
4.1 Route Between Nodes: Given a directed graph, design an algorithm to find out whether there is a
route between two nodes
- Approach 1: Brute force approach:
- Look a look at each nodes pointers values. If it doesn't exist, then look at those pointers pointers values. Accumulate this process over time. Search the pointers accumulated values over time, searching through this array everytime until your search is exhausted. If one or the other original nodes intersection in there values, then the result is true.
- Approach 2: Breadth first search
- Iterate through the graph, marking nodes as visited to avoid repetition.
- Notice how queue's are really nice in exploring and checking all adjacent nodes. Its a nice algorithm to know in general.
// great for lightweight labeling
enum State { Unvisited, Visiting, Visited };
bool isConnected(Graph g, Node *one, Node *two) {
// same node or no links
if (one == two || one.getAdjacent() == nullptr || two.getAdjacent() == nullptr)
return true;
// mark each node
for (Node i : g.getNodes()) {
i.state = State.Unvisited;
}
// base case
one.state = State.Visiting;
queue<Node*> explore;
explore.push(one);
Node *temp = new Node();
// explore adjacent node starting from arbitrary node
while (!explore.isEmpty()) {
// explore one node at a time, and its adjacent pairs
temp = explore.pop();
if (temp != nullptr) {
for (Node i : temp.getAdjacent()) {
if (i.state == State.Unvisted) {
if (i == two) return true;
i.state == State.Visiting;
explore.push(i);
}
}
}
temp.state = State.Visited;
}
return false;
}
4.2 Minimal Tree: Given a sorted (increasing order) array with unique integer elements, write an algorithm to create a binary search tree with minimal height.
- This algorithm can be solved by continuously taking the midpoint of the array and inserting it into the Binary search tree using level order insertion.
- Or even more simply, this algorithm follows a pre-order traversal pattern: ->access, ->left, -> right. We can apply this recursive procedure using our midpoint rule.
TreeNode createMinBST(int arr[]) {
createMinBST(int arr[], 0, sizeof(arr) / sizeof(arr[1]));
}
TreeNode createMinBST(int arr[], int start, int end) {
// leaf nodes point to null
if (start > end) return nullptr;
int midpoint = (end - start) / 2;
TreeNode *node = new TreeNode(midpoint);
// preorder: access, left, right
node->left = createMinBST(arr[], start, midpoint - 1);
node->right = createMinBST(arr[], midpoint + 1, end);
return node;
}
- I've referenced below an image that describes the way I went about this process.
- I've noticed that procedure of belowing the tree comes out to be a level order tranversal (or BFS). Each node represents an low and high that can calculate the index of nums to insert into the tree next. In addition every subsequential node after that is based on its previous.
bool isValidIndex(int low, int high, int size) {
return (low <= high && low >= 0 && low <= size - 1 && high >= 0 && high <= size - 1);
}
void build_min_tree(vector<int> &nums) {
if (nums.empty()) return;
queue<pair<int, int>> low_high;
int low = 0;
int high = nums.size() - 1;
int middle;
low_high.push(make_pair(low, high));
while (!low_high.empty()) {
pair<int, int> add_this = low_high.front();
low_high.pop();
middle = add_this.first + ((add_this.second - add_this.first) / 2);
cout << "index:" << middle << " (" << nums.at(middle) << " ) ";
// BST::insert(nums.at(middle));
// add the next two descendents depending on the previous
low = add_this.first;
high = middle - 1;
if (isValidIndex(low, high, nums.size())) {
low_high.push(make_pair(low, high));
}
low = middle + 1;
high = add_this.second;
if (isValidIndex(low, high, nums.size())) {
low_high.push(make_pair(low, high));
}
}
}
int main()
{
vector<int> nums = {0,1,2,3,4,5,6,7,8,9};
build_min_tree(nums);
pause();
nums = { 0,1,2,3,4,5,6,7,8,9,10,11,12,123,200,300, 2010 };
build_min_tree(nums);
pause();
}
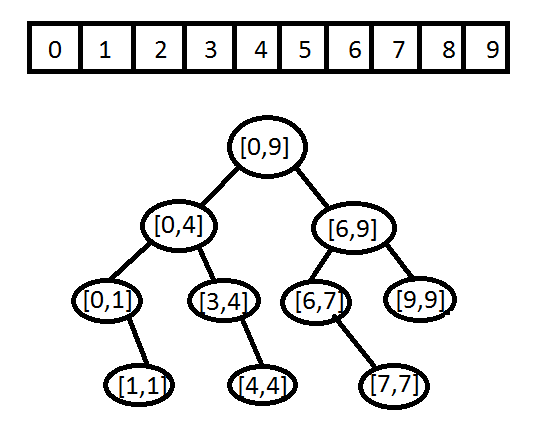
- This follows the BST route, albeit it has been modified to print out actually level by level.
- All that is required next of this is to simplify insert the elements printed out in the for loop.
void LL_BFS(Node *root) {
vector<Node*> current;
current.push_back(root);
while (!current.empty()) {
// print all the current entires
for (auto &i : current) {
cout << i->value << " ";
}
cout << endl;
// set up the next level
int prev_size = current.size();
for (int i = 0; i < prev_size; i++) {
// erase current node, and replace with its children
Node *temp = current.at(i);
if (temp->left)
current.push_back(temp->left);
if (temp->right)
current.push_back(temp->right);
}
// erase all old elements
current.erase(current.begin(), current.begin() + prev_size);
}
}
4.4 Check Balanced: Implement a function to check if a binary tree is balanced. For the purposes of this question, a balanced tree is defined to be a tree such that the heights of the two subtrees of any node never differ by more than one.
- Brainstorm:
- Reminded me of a post order traversal, where we recursively access individual subtrees, starting with the left.
bool checkBalance(TreeNode *root) {
return checkBalance(Treenode *root) != INT_MIN;
}
int checkBalance(TreeNode *root) {
if (root == nullptr) return -1;
int left = checkBalance(root->left);
if (left == INT_MIN) return INT_MIN;
int right = checkBalance(root->right);
if (right == INT_MIN) return INT_MIN;
if (abs(left - right) >= 2) {
return INT_MIN;
}
else {
return max(left, right) + 1;
}
}
4.5 Validate BST: Implement a function to check if a binary tree is a binary search tree.
- We can validate it through an inorder traversal
- O(2n) time and space
bool isBST(Node *root, vector<int> &ar) {
if (root) {
isBST(root->left, ar);
ar.push_back(root->value);
isBST(root->right, ar);
}
return is_sorted(ar.begin(), ar.end());
}
- We can speed things up a little by just checking the previous element as we go along
- O(n) time and space
int prev = INT_MIN;
bool isBST2(Node *root) {
if (root) {
isBST2(root->left);
if (prev > root->value) {
return false;
}
prev = root->value;
isBST2(root->right);
}
return true;
}
4.7 Build Order: You are given a list of projects and a list of dependencies (which is a list of pairs of projects, where the second project is dependent on the first project). All of a project's dependencies must be built before the project is. Find a build order that will allow the projects to be built. If there is no valid build order, return an error.
- The idea with this problem is to build a graph that represents the dependencies provided. However, the direction we chose to do so is important. In the example, (a d) implies that a is dependent on d, or we can write that as (a->d) in the graph. However, because we can trying to prioritize the things the depend on nothing first, then I chose to write it the other way (d->a). This, in the beginning, I will have dependencies f and e empty.
- Faults in this implementation: In my linked list implementation, I am lazy and havent bothered to handle memory leaks. Also, there is a more elegent solution to removal all element of val.
EXAMPLE
Input:
projects: a, b, c, d, e, f
dependencies: (a, d), (f, b), (b, d), (f, a), (d, c)
Output: f, e, a, b, d, c
class Node {
public:
Node(char val) : data(val) {
next = nullptr;
}
char data;
int weight;
Node *next;
};
class LL {
public:
LL() {
front = end = nullptr;
}
void push_back(char vertex) {
Node *newNode = new Node(vertex);
if (isEmpty()) {
front = end = newNode;
}
else {
end->next = newNode;
end = newNode;
}
}
void removeAll(char ch) {
if (isEmpty()) return;
// first element
Node *newFront = nullptr;
if (front->data != ch) {
newFront = front;
}
Node *newIter = newFront;
Node *iter = front;
iter = iter->next;
while (iter) {
if (iter->data != ch) {
if (newIter) {
newIter->next = iter;
newIter = iter;
}
else {
newIter = iter;
}
}
iter = iter->next;
}
if (newIter) {
newIter->next = nullptr;
}
front = newFront;
}
void print(Node *iter) {
if (!iter) return;
cout << iter->data << " -> ";
print(iter->next);
}
Node *front, *end;
private:
bool isEmpty() {
return front == nullptr;
}
};
// simulating friend network
class Graph {
public:
Graph(bool dir) : directed(dir), n_verticies(0), n_edges(0) {
}
void insertProjects(vector<char> &p) {
for (auto &i : p) {
LL *ll = new LL();
graph2.insert({ {i} ,{ll} });
}
}
void insertNodes(vector<pair<char, char>> &depend) {
for (auto &i : depend) {
auto &find = graph2.find(i.second);
if (find != graph2.end()) {
// insert first element, since found
find->second->push_back(i.first);
}
}
}
vector<char> definePriority(vector<char> &projects, vector<pair<char, char>> &depend) {
insertProjects(projects);
insertNodes(depend);
vector<char> priority;
// scan through list and find first null element
bool flag = true;
while (flag) {
flag = false;
for (auto &i : graph2) {
if (i.second->front == nullptr) {
tranverse();
priority.push_back(i.first);
removeAllDependancies(i.first);
// reset for loop and scan through again
flag = true;
break;
}
}
}
return priority;
}
void removeAllDependancies(char i) {
//graph2.find(i)->second->front = nullptr;
delete graph2.find(i)->second;
graph2.erase(i);
for (auto &j : graph2) {
j.second->removeAll(i);
}
}
void tranverse() {
for (auto &i : graph2) {
cout << i.first << " : ";
i.second->print(i.second->front);
cout << endl;
}
cout << endl;
//pause();
}
int getNumVert() { return n_verticies; }
int getNumEdges() { return n_edges; }
private:
bool directed;
int n_verticies, n_edges;
unordered_map<char, LL*> graph2;
};
int main()
{
Graph *friend_network = new Graph(true);
vector<char> projects = { 'a','b','c','d','e','f' };
vector<pair<char, char>> depend = {
{'a', 'd'},{ 'f', 'b' },{ 'b', 'd' },{ 'f', 'a' },{ 'd', 'c' }
};
vector<char> priority = friend_network->definePriority(projects, depend);
print(priority);
}
4.8 First Common Ancestor: Design an algorithm and write code to find the first common ancestor of two nodes in a binary tree. Avoid storing additional nodes in a data structure. NOTE: This is not necessarily a binary search tree.
- This problem is similar to finding the intersection of two linked lists.
- The first common ancestor of two nodes is also the first intersections of two nodes in a binary tree.
- I am going to assume that each node has accessibility to its parent.
- As a reminder, depth measures the number of edges a particular node has to its root, while the height of a tree measure the number of edges a particular node has to its deepest leaf. We use depth to measure distance because we are going to be traversing UP the tree, rather than down.
struct Node {
int val;
Node *left;
Node *right;
Node *parent;
Node(int x, Node *p) :
val(x), left(NULL), right(NULL), parent(p) {}
};
Node* firstCommonAncestor(Node *one, Node* two) {
if (!one || !two) return nullptr;
int distance = depth(one) - depth(two);
// if (-), then two is larger, so increment it first, and vise-versa
if (distance < 0) {
for (int i = 0; i < abs(distance); i++) {
two = two->parent;
}
// now increment at the same time
while (one != two) {
one = one->parent;
two = two->parent;
}
}
else {
for (int i = 0; i < abs(distance); i++) {
one = one->parent;
}
// now increment at the same time
while (one != two) {
one = one->parent;
two = two->parent;
}
}
return one; // or two
}
int depth(Node *node) {
int depth = 0;
while (node->parent) {
depth++;
node = node->parent;
}
return depth;
}
- Now I am going to assume that the the parent of each node is not in the Object of
Node.
struct Node {
int val;
Node *left;
Node *right;
Node(int x) : val(x), left(NULL), right(NULL) {}
};
- Now I am going to assume that the the parent of each node is not in the Object of
Node. - The idea goes as follows:
- First we check the base condition: we will assume that a node cannot be a descendent of itself. So that if both nodes are shared across the same linage, then will return null. This is what the first condition checks for. Either the root is null to begin with or q contains p or p contains q.
- Now we can step into the recursive condition: but we first have to understand the following:
- One, the root is always the highest common ancestor of all nodes, since all nodes can trace their linage all the way up to the root.
- Two, the first instance starting from the root that q and p a are on different sides of the tree, we know the root is the lowest common ancestor. This is because all the previous ancestoral nodes before are were some level of the highest common ancestor.
- So the question now lyes: what part of the tree do we descend down? Well, if
p_contained_in_left != q_contained_in_right, it could either be one of the two:!p_contained_in_left == q_contained_in_rightor!q_contained_in_right == p_contained_in_left. The first one says that both p and q are contained in the right child of the subtree. The second one says both p and q are contained in the left child of the subtree. So we always continue to descend down the tree that contains both p and q.
Node* lowestCommonAncestor(Node* root, Node* p, Node* q)
{
if (!root || contains(p, q) || contains(q, p))
return nullptr;
return lowestCommonAncestor_helper(root, p, q);
}
Node* lowestCommonAncestor_helper(Node *root, Node *p, Node *q)
{
bool p_contained_in_left = contains(root->left, p);
bool q_contained_in_right = contains(root->right, q);
if (p_contained_in_left == p_contained_in_left)
return root;
if (!p_contained_in_left == q_contained_in_right)
lowestCommonAncestor_helper(root->right, p, q);
else if (p_contained_in_left == !q_contained_in_right)
lowestCommonAncestor_helper(root->left, p, q);
}
bool contains(Node *root, Node *_this)
{
if (!root) return false;
else if (root == _this) return true;
return contains(root->left, _this) || contains(root->right, _this);
}
4.9 BST Sequences: A binary search tree was created by traversing through an array from left to right and inserting each element. Given a binary search tree with distinct elements, print all possible arrays that could have led to this tree.
Ex.
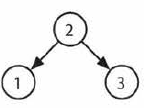
Output: {2, 1, 3}, {2, 3, 1}- Brain storm:
- I first noticed that a pre order traversal nicely prints out a possible combination of the array. I can use this transversal once, and use the output array as the basis of the remainder of my combinations depending on a few properties.
- I will have a level order traversal, which will check to see if has another sibling (same parent), by using the property of B-trees that children with siblings are expected to grow by 2^n in pairs of two per level. In a binary configuration, this will determine whether the number is flippable in the combination.
- num unique flips = log_2(num flippables)
- Each unique flip can be expressed as a combination on the number of states
- num combination states = 2^(unique flip), an even number
- In my pre-order tranversal array, each unique flip occurs with the next proceeding flip, and this will produce another combination based on the pre order combination.
- Then, using each uniquely flipped array, we can write as a combination of the others, discluding itself and the preorder combination.
- BigO:
- Preorder traversal O(N)
- Parent check O(2N)
vector<int> sameParentLevelTrav(Node *root) {
vector<int> siblings;
queue<Node *> q;
Node *temp = new Node();
q.push(root);
int completeTreeCounter = 1;
while (!q.isEmpty()) {
temp = q.front();
q.pop();
// complete tree - siblings exist
if (temp->left != null and temp->right != null) {
siblings.push(temp->left->value);
siblings.push(temp->right->value);
}
if (temp->left != null) {
q.push(temp->left);
}
if (temp->right != null) {
q.push(temp->right);
}
}
}
vector<int> preOrder(Node *root) {
// assumming vector<int> preOrderNums is accessable in the class
if (root != nullptr) {
preOrderNums.push_back(root->value);
preOrder(root->left);
preOrder(root->right);
}
return preOrderNums;
}
vector<int> uniqueSwap(int one, int two, vector<int> &base) {
}
vector<vector<int>> BSTcombinations(Node *root) {
vector<vector<int>> finalComb;
// preorder array
vector<int> preArr = preOrder(root);
finalComb.push_back(preArr);
// analyize siblings
vector<int> siblings = sameParentLevelTrav(root);
vector<int> temp = preArr;
// find unique combinations
int swap1_i = 0;
int swap2_i = 1;
while (swap2_i > siblings.size()) {
int swap1 = siblings.at(swap1_i);
int swap2 = siblings.at(swap2_i);
// find where index exists
int j;
for (j = 0; j < temp.size(); j++) {
if (temp.at(j) == swap1) {
break;
}
}
// find where index exists
int k;
for (k = 0; k < temp.size(); k++) {
if (temp.at(k) == swap2) {
break;
}
}
// preform swap -> iter_swap <algorithm>
iter_swap(temp.begin() + j, temp.begin() + k);
finalComb.push_back(temp);
// next iteration
temp = preArr;
swap1_i += 2;
swap2_i += 2;
}
// find remaining combinations
for (int i = 0; i < pow(2, finalComb.size() - 1); i++) {
}
}
More efficient and complete implementation
4.10 Check Subtree: Tl and T2 are two very large binary trees, with Tl much bigger than T2. Create an algorithm to determine if T2 is a subtree of Tl. A tree T2 is a subtree of T1 if there exists a node n in Tl such that the subtree of n is identical to T2 . That is, if you cut off the tree at node n, the two trees would be identical.
Method 1:
- With this method, I am using the idea that within a preorder traversal, a subtree exists if within said tranversal exists the consecutive sequence of values of the subtree.
- However, we must indicate null elements in the tree because in doing so we preverse the entire uniqueness of a tree. Then we compare two preorder traversals with the null elements included, we ensure a subtree exists when they both preserve the same values and null elements.
template<typename iter>
bool isEqual(iter main_start, vector<int> &nums) {
for (int i = 0; i < nums.size(); i++) {
if (*(main_start + i) != nums.at(i)) {
return false;
}
}
return true;
}
// testing if nums2 is subarray of nums1
bool isSubArray(vector<int> &main, vector<int> &nums) {
for (int j = 0; j < main.size() - nums.size() + 1; j++)
if (isEqual(main.begin() + j, nums))
return true;
return false;
}
void preOrderTrav(Node *root, vector<int> &ar) {
if (!root) {
ar.push_back(INT_MAX);
return;
}
ar.push_back(root->value);
preOrderTrav(root->left, ar);
preOrderTrav(root->right, ar);
}
bool isSubtree(Node *root1, Node *root2) {
vector<int> tree1, tree2;
preOrderTrav(root1, tree1);
preOrderTrav(root2, tree2);
print(tree1);
print(tree2);
return isSubArray(tree1, tree2);
}
- Disadvantages:
- O(N) to traverse, O(N) extra memory, and then O(N^2) to check subarray.
- Lets try and get rid of that N^2!
- Method 2:
- This method checks to see whether or two trees are the same on the basis that their addresses are the same. So while it doesnt work with two independent trees, it will work with the same tree.
- O(N) time and space.
- I've modified the subtree comparison by simply finding first element of the preorder tranversal of the second tree, and then confirming the remainder of the sequence. This will work with duplicate elements, since the addresses are unique.
template<typename iter>
bool isEqual(iter main_start, vector<Node*> &nums) {
for (int i = 0; i < nums.size(); i++) {
if (&(*(main_start + i)) != &nums.at(i)) {
return false;
}
}
return true;
}
int find(vector<Node*> &nums, Node* findthis) {
for (int i = 0; i < nums.size(); i++) {
if (&nums.at(i) == &findthis) {
return i;
}
}
return INT_MAX;
}
// testing if nums2 is subarray of nums1
bool isSubArray(vector<Node*> &main, vector<Node*> &nums) {
int index = find(main, nums.at(0));
if (index == INT_MAX) return false;
else {
// confirm the rest of the sequence
return isEqual(main.begin() + index, nums);
}
}
void preOrderTrav(Node *root, vector<Node*> &ar) {
if (!root) {
ar.push_back(nullptr);
return;
}
ar.push_back(root);
preOrderTrav(root->left, ar);
preOrderTrav(root->right, ar);
}
bool isSubtree(Node *root1, Node *root2) {
vector<Node*> tree1, tree2;
preOrderTrav(root1, tree1);
preOrderTrav(root2, tree2);
print(tree1);
print(tree2);
return isSubArray(tree1, tree2);
}
- To make this work with two independent subtrees, I've modified it to take in the values instead.
- This may not work with nodes in a tree that contain duplicate elements!
template<typename iter>
bool isEqual(iter main_start, vector<int> &nums) {
for (int i = 0; i < nums.size(); i++) {
if (*(main_start + i) != nums.at(i)) {
return false;
}
}
return true;
}
int find(vector<int> &nums, int findthis) {
for (int i = 0; i < nums.size(); i++) {
if (nums.at(i) == findthis) {
return i;
}
}
return INT_MIN;
}
// testing if nums2 is subarray of nums1
bool isSubArray(vector<int> &main, vector<int> &nums) {
int index = find(main, nums.at(0));
if (index == INT_MIN) return false;
else {
// confirm the rest of the sequence
return isEqual(main.begin() + index, nums);
}
}
void preOrderTrav(Node *root, vector<int> &ar) {
if (!root) {
ar.push_back(INT_MAX);
return;
}
ar.push_back(root->value);
preOrderTrav(root->left, ar);
preOrderTrav(root->right, ar);
}
bool isSubtree(Node *root1, Node *root2) {
vector<int> tree1, tree2;
preOrderTrav(root1, tree1);
preOrderTrav(root2, tree2);
print(tree1);
print(tree2);
return isSubArray(tree1, tree2);
}
4.11 Random Node: You are implementing a binary search tree class from scratch, which, in addition to insert, find, and delete, has a method getRandomNode() which returns a random node from the tree. All nodes should be equally likely to be chosen. Design and implement an algorithm for getRandomNode, and explain how you would implement the rest of the methods.
- My getRandNode assumes that our bst has kept track of the max level. I use this variable to indicate to the tree how far we should go down as a random index.
- Then, whilst tranversing the tree recursively, I keep track of this count, and simply join a random left or right.
Node* tranverseRand(Node *root, int level, int count) {
if (level <= count) return root;
cout << root->value << endl;
pause();
srand(time(nullptr));
bool direction = rand() % 1;
if (root->right && direction)
tranverseRand(root->right, level, ++count);
else if(root->left && !direction)
tranverseRand(root->left, level, ++count);
// otherwise just take the path that exists
else if (root->right)
tranverseRand(root->right, level, ++count);
else
tranverseRand(root->left, level, ++count);
}
Node* getRandomNode(Node *root, int maxLevel) {
if (!root) return nullptr;
srand(time(nullptr));
int level = rand() % maxLevel; // [0 - maxLevel]
return tranverseRand(root, level, 0);
}
- However, while this approach is fast, it doesnt represent the nodes equally. It would if the left and right sides were the same size, but it is likely not the case. We cannot have left and right be chosen on a 50/50 likelyhood. If the left side contains more nodes, it would be represented as more likely to go left.
- To fix this, what we can do is maintain the size of the left and right subtree PER node. At this point, we would then be able to rightfully balance the probabilities of the left and right subtrees.
Node* tranverseRand(Node *root, int level, int count) {
if (level <= count) return root;
bool direction = rand() % root->size;
if (root->right && direction > root->leftsize)
tranverseRand(root->right, level, ++count);
else if(root->left && direction <= root->leftsize)
tranverseRand(root->left, level, ++count);
// otherwise just take the path that exists
else if (root->right)
tranverseRand(root->right, level, ++count);
else
tranverseRand(root->left, level, ++count);
}
Node* getRandomNode(Node *root, int maxLevel) {
if (!root) return nullptr;
srand(time(nullptr));
int level = rand() % maxLevel; // [0 - maxLevel]
return tranverseRand(root, level, 0);
}
Node* tranverseRand(Node *root, int level, int count) {
if (level <= count) return root;
bool direction = rand() % root->size;
if (root->right && direction > root->leftsize)
tranverseRand(root->right, level, ++count);
else if(root->left && direction <= root->leftsize)
tranverseRand(root->left, level, ++count);
// otherwise just take the path that exists
else if (root->right)
tranverseRand(root->right, level, ++count);
else
tranverseRand(root->left, level, ++count);
}
Node* getRandomNode(Node *root, int maxLevel) {
if (!root) return nullptr;
srand(time(nullptr));
int level = rand() % maxLevel; // [0 - maxLevel]
return tranverseRand(root, level, 0);
}
- An a lot simpler approach would be to just tranverse (any traversal) the tree until we reach a random index n. Where n is 0 % size_tree.
int getRandomInt(int size) {
srand