Pattern Matching

16.18 Pattern Matching: You are given two strings, pattern and value. The pattern string consists of just the letters a and b, describing a pattern within a string. For example, the string cat catgoc at go matches the pattern aabab (where cat is a and go is b). It also matches patterns like a, ab, and b. Write a method to determine if value matches pattern.

• Brute Force:

  • Generate all possible substrings of the value. This will generate n^2 different 'words'. Then, with these these words, pair it up with all the substrings. This will generate n^4 pairs. Now using each pair of substrings, pass it into a function that use these pairs as the two distinguishing strings, and determine whether or not it matches the sequence pattern.

• Optimized:

  • There are some basic cases we can eliminate:

    • If the value is empty or if the pattern exceeds the value, is it always false.

    • If the pattern is 1 char, then we know that it can represent any 'word', so set to true

  • With the remainder of the cases, one thing we can do is generate the number of valid combinations. This is best demonstrated with an example.

• If we're given pattern = aabaa and value=catcatgocatcat

• Then are are only so many patterns (number of characters) that we can define to a and b, just that they make out the full sequence of the string.

A = freq(a) = 4
B = freq(b) = 1
l = length = 14

a = number of letters assigned to a
b = number of letters assigned to b

Aa + Bb = l
b = (l - Aa) / B
4a + b = 14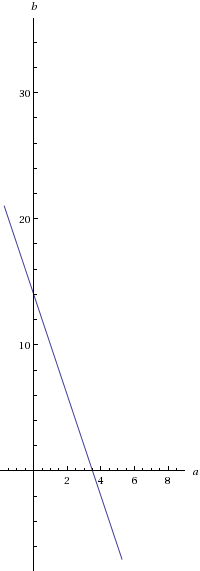

• Now we have an infinity number of solutions that are defined by this number line. We can constrain it in the following ways:

  • Valid solutions must be in the top left quadrant of the cartisian plane, since we need a and b to both be positive.

  • Both a and b must exist at least once so $a \neq b \neq 0$ because we cannot have zero characters.
  • a must be defined from $1 \leq a \leq zero(b)$ and b defined $1 \leq b \leq zero(a)$ because of the two statements above.
  • Both a and b must be discrete values (we cannot have half a character). To test for discrete values, we must check for whole numbers from $1 \leq a \leq zero(b)$ .
• On this number line, we are given 3 possibilities:

  • (1,10), (2,6), (3,2)

• Testing our solution:

  • (1,10) implies that a = value.at(0) = c, then a = value.at(1) = a, so invalid.

  • (2,6) == a = ca; tc; so invalud

  • and finally (3,2); cat ; cat; cat; go; cat; cat (valid)

class Line {
public:
    Line(double length, double freq_a, double freq_b) {
        // edge cases, (vertical or horizontal lines)
        // then there is only 1 valid point
        // vertical
        bool flag = true;
        if (freq_b == 0) {
            valid_points.push_back({ { int(length / freq_a) },{ 0 } });
            flag = false;
        }
        // horizontal
        if (freq_a == 0) {
            valid_points.push_back({ { 0 },{ int(length / freq_b) } });
            flag = false;
        }

        if (flag) {
            // solving for b
            y_int = length / freq_b;
            slope = freq_a / freq_b;

            // finding zeros 0 = l - Aa / B simplifies to
            zero_a = length / freq_a;
            zero_b = length / freq_b;

            // defining all valid points - using floor ensures a non negative number
            for (double i = 1; i < zero_a; i++) {
                // b = l - Aa / B
                double y = length / freq_b - (freq_a * i) / freq_b;
                // check for whole number
                if (y == int(y)) {
                    valid_points.push_back({ { int(i) },{ int(y) } });
                }
            }
        }

    }


    vector<pair<int, int>> valid_points;

private:
    float y_int, slope;
    double zero_a, zero_b;
};


bool check_if_valid_point(pair<int, int> &point, string pattern, string value) {
    string interp_a = "";
    string interp_b = "";
    string last_a, last_b;
    int count = 0;

    for (int i = 0; i < pattern.length(); i++) {
        if (pattern.at(i) == 'a') {
            for (int i = 0; i < point.first; i++) {
                interp_a += value.at(count++);
            }
            if (!last_a.empty() && last_a != interp_a) {
                return false;
            }
            last_a = interp_a;
            interp_a = "";
        }
        else {
            for (int i = 0; i < point.second; i++) {
                interp_b += value.at(count++);
            }
            if (!last_b.empty() && last_b != interp_b) {
                return false;
            }
            last_b = interp_b;
            interp_b = "";
        }
    }
    return true;
}

bool pattern_match(string pattern, string value) {
    // pattern cannot exceed value
    if (pattern.empty() || value.empty() || 
        pattern.size() > value.size()) return false;

    // a and b are ambigious and value is not empty
    else if (pattern.length() == 1) return true;

    // algorithm:
    // 1) Find frequencies of a and b
    double freq_a = 0, freq_b = 0;
    double length = value.length();
    for (auto i : pattern) {
        if (i == 'a') freq_a++;
        else if (i == 'b') freq_b++;
    }

    // 2) Define the line and check for valid points
    Line line(value.length(), freq_a, freq_b);
    vector<pair<int, int>> points = line.valid_points;
    for (auto &i : points) {
        if (check_if_valid_point(i, pattern, value)) {
            return true;
        }
    }
    return false;
}


int main() {
    cout << boolalpha << pattern_match("aabaa", "catcatgocatcat") << endl;
    cout << boolalpha << pattern_match("bbabb", "catcatgocatcat") << endl;
    cout << boolalpha << pattern_match("aba", "catgocat") << endl;
    cout << boolalpha << pattern_match("aab", "catcatgo") << endl;
    cout << boolalpha << pattern_match("bbaba", "dandandavdandav") << endl;
    cout << boolalpha << pattern_match("aaa", "catcatcat") << endl;

    cout << boolalpha << pattern_match("aabba", "catcatgocatcat") << endl;
    cout << boolalpha << pattern_match("baabb", "catcatgocatcat") << endl;
    cout << boolalpha << pattern_match("abb", "catgocat") << endl;
    cout << boolalpha << pattern_match("abb", "catcatgo") << endl;
    cout << boolalpha << pattern_match("bbb", "catcatgo") << endl;