Coins
8.11 Coins: Given an infinite number of quarters (25 cents), dimes (10 cents), nickels (5 cents), and pennies (1 cent), write code to calculate the number of ways of representing n cents.
I first decided to take the brute force approach. It runs fine, but the solution isnt correct. I still include it because I think the idea is valuable.
What I did is take the power set of the permutations to find all the possible subcombinations, and their permutations. After generating these, (which there are a reletively few number of, as QDNP is only 4 characters, and the power set grows at 2^k, which perms at k!) this only generates 65 different permutations of subcombinations.
I then ran these through a function that would mod all the elements in their strict order in order to find the ones that work (generate change == 0).
The main problem with this is that now each 'command' has to be iterated through a several number of different times. E.g. "DQ" does not only mean maxing out Dimes and then Quarters, as my algorithm does. It means finding and all combinations of n-number of dimes, and n-number of quarters.
// wrong!
void permute_rec(vector<string> &cur_perms, string fullstr, int index) {
if (index >= fullstr.length()) return;
// add char for every word of every index
vector<string> newPerms;
for (auto i : cur_perms) {
string go_back = i;
for (int j = 0; j <= i.length(); j++) {
char add = fullstr.at(index);
i.insert(i.begin() + j, add);
newPerms.push_back(i);
i = go_back;
}
}
cur_perms = newPerms;
permute_rec(cur_perms, fullstr, ++index);
}
vector<string> permute(string str) {
vector<string> permutations;
if (str.empty()) return permutations;
// start us off
permutations.push_back(string(1, str.at(0)));
if (str.length() <= 1) return permutations;
// go
permute_rec(permutations, str, 1);
return permutations;
}
vector<string> power_set(string str) {
vector<string> build;
build.push_back(" ");
if (str.length() >= 1) {
string temp(1, str[0]);
build.push_back(temp);
}
for (int i = 1; i < str.length(); i++) {
int cur_size = build.size();
for (int j = 0; j < cur_size; j++) {
string temp = build[j];
if (temp == " ")
temp = str[i];
else
temp.insert(temp.end(), str[i]);
//print(build);
build.push_back(temp);
}
}
return build;
}
unordered_map<string, vector<int>> successful_commands(vector<vector<string>> &all_commands, int change) {
unordered_map<string, vector<int>> successes;
vector<int> poten_success;
int chg_cpy = change;
int remainder;
for (int i = 0; i < all_commands.size(); i++) {
for (int j = 0; j < all_commands.at(i).size(); j++) {
string cur_command = all_commands.at(i).at(j);
for (int k = 0; k < cur_command.length(); k++) {
if (cur_command.at(k) == 'Q') {
poten_success.push_back(int(change / 25));
change = change % 25;
}
else if (cur_command.at(k) == 'D') {
poten_success.push_back(int(change / 10));
change = change % 10;
}
else if (cur_command.at(k) == 'N') {
poten_success.push_back(int(change / 5));
change = change % 5;
}
else if (cur_command.at(k) == 'P') {
poten_success.push_back(int(change / 1));
change = change % 1;
}
// if the change reaches zero before the end of cur_str
if (change == 0 && k + 1 < cur_command.length()) {
poten_success.clear();
change = chg_cpy;
k = cur_command.length();
//continue;
}
}
// only add to hash map if it fully emitted the change
if (change == 0) {
successes.insert({ { cur_command } ,{ poten_success } });
}
poten_success.clear();
change = chg_cpy;
}
}
return successes;
}
unordered_map<string, vector<int>> optional_change(int change) {
unordered_map<string, vector<int>> results;
if (change == 0) return results;
// quarters, dimes, nickels, pennies
vector<string> comb_commands = power_set("QDNP");
vector<vector<string>> all_commands;
for (auto i : comb_commands) {
all_commands.push_back(permute(i));
}
print2d(all_commands);
return successful_commands(all_commands, change);
}
void map_print(unordered_map<string, vector<int>> &map) {
for (auto &i : map) {
cout << i.first << ": ";
for (auto j : i.second) {
cout << j << ", ";
}
cout << endl;
}
cout << endl;
pause();
}
int main() {
unordered_map<string, vector<int>> change = optional_change(100);
//printing re
map_print(change);
}New approach:
Given just 3 different coins, we can represent this problem visually:
Some combination of 25, 10, and 5 to represent a 3-dimensional plane.
If each distinct integer of the plane
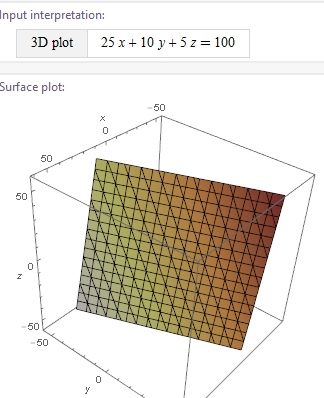
However when we limit the graph to its realistic dimensions
ContourPlot3D[25 x+10 y+5 z==100, {x, 0, 22}, {y, 0, 22}, {z, 0, 22}], we get something like this:
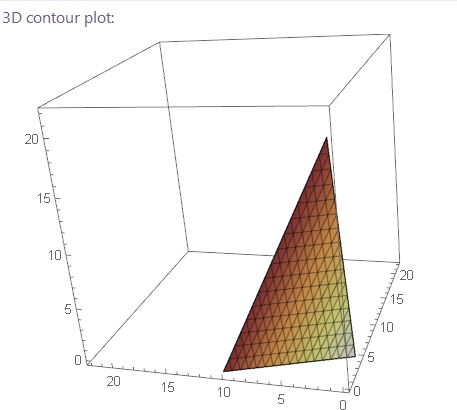
Which contains a limited surface area we can calculate. Each distinct whole number point represents a solution. So the surface area represents the total sum of solutions.
The surface area is a double integral...
Can apply the same idea with in a 4 dimensional solution, like the problem asks.
Last updated
Was this helpful?