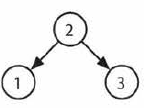
BST Sequences

4.9 BST Sequences: A binary search tree was created by traversing through an array from left to right and inserting each element. Given a binary search tree with distinct elements, print all possible arrays that could have led to this tree.

Ex.

Output: {2, 1, 3}, {2, 3, 1}

• Brain storm:

  • I first noticed that a pre order traversal nicely prints out a possible combination of the array. I can use this transversal once, and use the output array as the basis of the remainder of my combinations depending on a few properties.

  • I will have a level order traversal, which will check to see if has another sibling (same parent), by using the property of B-trees that children with siblings are expected to grow by 2^n in pairs of two per level. In a binary configuration, this will determine whether the number is flippable in the combination.

    • num unique flips = log_2(num flippables)

    • Each unique flip can be expressed as a combination on the number of states

      • num combination states = 2^(unique flip), an even number

  • In my pre-order tranversal array, each unique flip occurs with the next proceeding flip, and this will produce another combination based on the pre order combination.

  • Then, using each uniquely flipped array, we can write as a combination of the others, discluding itself and the preorder combination.

  • BigO:

    • Preorder traversal O(N)

    • Parent check O(2N)

vector<int> sameParentLevelTrav(Node *root) {
    vector<int> siblings;
    queue<Node *> q;
    Node *temp = new Node();
    q.push(root);

    int completeTreeCounter = 1;

    while (!q.isEmpty()) {
        temp = q.front();
        q.pop();

        // complete tree - siblings exist
        if (temp->left != null and temp->right != null) {
            siblings.push(temp->left->value);
            siblings.push(temp->right->value);
        }

        if (temp->left != null) {
            q.push(temp->left);
        }

        if (temp->right != null) {
            q.push(temp->right);
        }
    }
}

vector<int> preOrder(Node *root) {
    // assumming vector<int> preOrderNums is accessable in the class
    if (root != nullptr) {
        preOrderNums.push_back(root->value);
        preOrder(root->left);
        preOrder(root->right);
    }
    return preOrderNums;
}

vector<int> uniqueSwap(int one, int two, vector<int> &base) {

}

vector<vector<int>> BSTcombinations(Node *root) {
    vector<vector<int>> finalComb;

    // preorder array
    vector<int> preArr = preOrder(root);
    finalComb.push_back(preArr);

    // analyize siblings
    vector<int> siblings = sameParentLevelTrav(root);
    vector<int> temp = preArr;

    // find unique combinations
    int swap1_i = 0;
    int swap2_i = 1;
    while (swap2_i > siblings.size()) {

        int swap1 = siblings.at(swap1_i);
        int swap2 = siblings.at(swap2_i);

        // find where index exists
        int j;
        for (j = 0; j < temp.size(); j++) {
            if (temp.at(j) == swap1) {
                break;
            }
        }

        // find where index exists
        int k;
        for (k = 0; k < temp.size(); k++) {
            if (temp.at(k) == swap2) {
                break;
            }
        }

        // preform swap -> iter_swap <algorithm>
        iter_swap(temp.begin() + j, temp.begin() + k);
        finalComb.push_back(temp);

        // next iteration
        temp = preArr;
        swap1_i += 2;
        swap2_i += 2;
    }

    // find remaining combinations
    for (int i = 0; i < pow(2, finalComb.size() - 1); i++) {

    }
}

More efficient and complete implementation