Minimal Tree

4.2 Minimal Tree: Given a sorted (increasing order) array with unique integer elements, write an algorithm to create a binary search tree with minimal height.

• This algorithm can be solved by continuously taking the midpoint of the array and inserting it into the Binary search tree using level order insertion.

• Or even more simply, this algorithm follows a pre-order traversal pattern: ->access, ->left, -> right. We can apply this recursive procedure using our midpoint rule.

TreeNode createMinBST(int arr[]) {
    createMinBST(int arr[], 0, sizeof(arr) / sizeof(arr[1]));
}

TreeNode createMinBST(int arr[], int start, int end) {
    // leaf nodes point to null
    if (start > end) return nullptr;

    int midpoint = (end - start) / 2;
    TreeNode *node = new TreeNode(midpoint);

    // preorder: access, left, right
    node->left = createMinBST(arr[], start, midpoint - 1);
    node->right = createMinBST(arr[], midpoint + 1, end);
    return node;
}

• I've referenced below an image that describes the way I went about this process.

• I've noticed that procedure of belowing the tree comes out to be a level order tranversal (or BFS). Each node represents an low and high that can calculate the index of nums to insert into the tree next. In addition every subsequential node after that is based on its previous.

bool isValidIndex(int low, int high, int size) {
    return (low <= high && low >= 0 && low <= size - 1 && high >= 0 && high <= size - 1);
}


void build_min_tree(vector<int> &nums) {
    if (nums.empty()) return;
    queue<pair<int, int>> low_high;
    int low = 0;
    int high = nums.size() - 1;
    int middle;

    low_high.push(make_pair(low, high));

    while (!low_high.empty()) {
        pair<int, int> add_this = low_high.front();
        low_high.pop();

        middle = add_this.first + ((add_this.second - add_this.first) / 2);
        cout << "index:" << middle << " (" << nums.at(middle) << " )  ";
        // BST::insert(nums.at(middle));

        // add the next two descendents depending on the previous
        low = add_this.first;
        high = middle - 1;

        if (isValidIndex(low, high, nums.size())) {
            low_high.push(make_pair(low, high));
        }

        low = middle + 1;
        high = add_this.second;

        if (isValidIndex(low, high, nums.size())) {
            low_high.push(make_pair(low, high));
        }
    }
}


int main()
{
    vector<int> nums = {0,1,2,3,4,5,6,7,8,9};
    build_min_tree(nums);
    pause();

    nums = { 0,1,2,3,4,5,6,7,8,9,10,11,12,123,200,300, 2010 };
    build_min_tree(nums);
    pause();
}

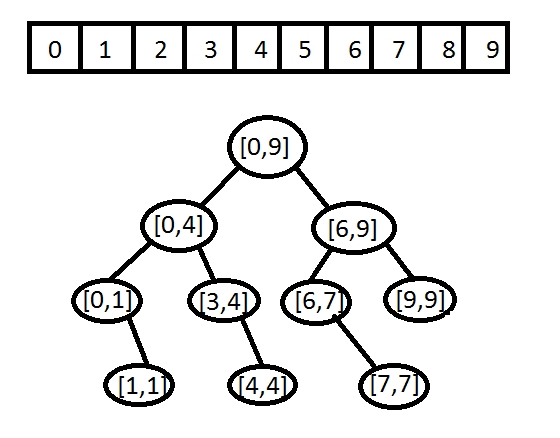
• This follows the BST route, albeit it has been modified to print out actually level by level.

• All that is required next of this is to simplify insert the elements printed out in the for loop.

    void LL_BFS(Node *root) {
        vector<Node*> current;
        current.push_back(root);

        while (!current.empty()) {
            // print all the current entires
            for (auto &i : current) {
                cout << i->value << "   ";
            }
            cout << endl;

            // set up the next level
            int prev_size = current.size();
            for (int i = 0; i < prev_size; i++) {
                // erase current node, and replace with its children
                Node *temp = current.at(i);
                if (temp->left)
                    current.push_back(temp->left);

                if (temp->right)
                    current.push_back(temp->right);
            }
            // erase all old elements
            current.erase(current.begin(), current.begin() + prev_size);
        }
    }